Thermografie Theorie – Physikalische Grundlagen
Das Prinzip der Infrarot-Thermografie beruht auf dem physikalischen Phänomen, dass jeder Körper mit einer Temperatur oberhalb des absoluten Nullpunktes (-273,15 °C) elektromagnetische Strahlung aussendet. Zwischen der Oberflächentemperatur eines Körpers und der Intensität und spektralen Zusammensetzung der von ihm ausgesandten Strahlung besteht dabei ein eindeutiger Zusammenhang. Durch die Ermittlung der Strahlungsintensität kann somit die Temperatur eines Objekts berührungslos bestimmt werden.

Einordnung im elektromagnetischen Spektrum
Infrarotstrahlung ist jener Teil des elektromagnetischen Spektrums, der sich an der langwelligen Seite des sichtbaren Spektrums an das rote Licht bei einer Wellenlänge von ca. 760 nm anschließt und sich bis zu etwa 1 mm Wellenlänge erstreckt.
Für die technische Temperaturmessung ist dabei der Bereich bis etwa 20 µm Wellenlänge von Bedeutung.
In der zweiten Hälfte des 19. Jahrhunderts gelang die Erkenntnis, dass Wärmestrahlung und andere elektromagnetische Wellen wie sichtbares Licht oder Radiowellen wesensgleich sind. Dem folgte die Entdeckung der Strahlungsgesetze durch KIRCHHOFF, STEFAN, BOLTZMANN, WIEN und PLANCK. Gegen Mitte des 20. Jahrhunderts war es dann im Ergebnis intensiver Arbeiten zur militärischen Nutzung der Infrarottechnik gelungen, erste Infrarot-Sichtgeräte zu bauen. Mit einigem zeitlichen und technologischen Abstand waren dann in den 60er Jahren auch die ersten Thermografiegeräte für den nichtmilitärischen Bereich verfügbar. Parallel hierzu, jedoch mit deutlich größerer Vielfalt der verfügbaren Geräte, vollzog sich die Entwicklung der Pyrometrie zu einem verbreiteten Verfahren der Temperaturmessung in der Industrie.
Strahlungsgesetze des Schwarzen Strahlers
Die in der Praxis vorkommenden Körper weisen sehr vielfältige Strahlungseigenschaften auf. So hat es sich bewährt, zunächst die vereinfachten Gesetzmäßigkeiten für einen Modellkörper mit idealen Strahlungseigenschaften zu betrachten, um sie dann auf die real vorkommenden Objekte anzuwenden. Dieser Modellkörper ist in der Strahlungsphysik der Schwarze Strahler. Er zeichnet sich dadurch aus, dass er von allen Körpern gleicher Temperatur die größtmögliche Intensität der ausgesandten Strahlung aufweist.
Die spektrale Verteilung der von einem Schwarzen Strahler ausgesandten Strahlung wird durch das PLANCKsche Strahlungsgesetz beschrieben:
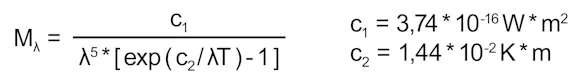
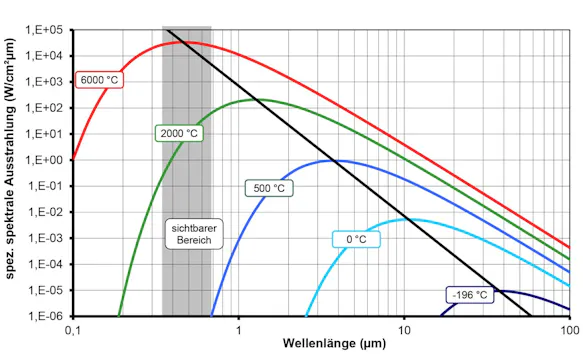
Aus dieser Darstellung ist erkennbar, dass die spektrale Zusammensetzung der ausgesandten Strahlung mit der Objekttemperatur variiert. So senden beispielsweise Körper mit Temperaturen von 500 °C auch Strahlungsanteile im sichtbaren Bereich aus. Weiterhin ist festzustellen, dass bei jeder Wellenlänge die Strahlungsintensität bei steigender Temperatur zunimmt.
Das PLANCKsche Strahlungsgesetz stellt den grundlegenden Zusammenhang für die berührungslose Temperaturmessung dar. Aufgrund seiner Abstraktion ist er jedoch für viele praktische Berechnungen in dieser Form nicht direkt anwendbar. Aus ihm lässt sich jedoch eine Vielzahl weiterer Zusammenhänge ableiten, von denen zwei im Folgenden kurz benannt werden sollen. So erhält man durch Integration der spektralen Strahlungsintensität über alle Wellenlängen den Wert für die gesamte vom Körper ausgesandte Strahlung. Dieser Zusammenhang wird als STEFAN-BOLTZMANNsches Gesetz bezeichnet.

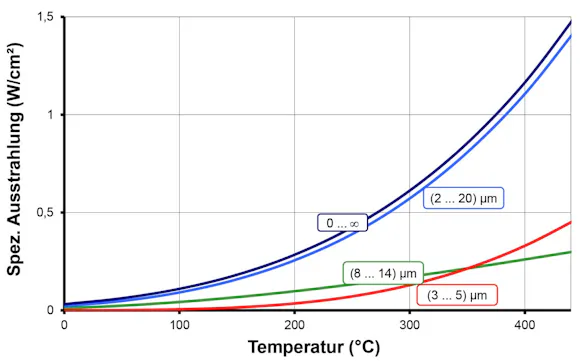
Aufgrund des einfachen mathematischen Zusammenhanges eignet es sich sehr gut zu Abschätzungen insbesondere bei Berechnungen zum Wärmehaushalt von Objekten sowie für die Zusammenhänge bei Gesamtstrahlungspyrometern. Der spektrale Messbereich der meisten Messgeräte ist jedoch üblicherweise stark begrenzt. Somit diese Gleichung hierfür nicht anwendbar.
Aus der grafischen Darstellung des PLANCKschen Strahlungsgesetzes wird ersichtlich, dass sich die Wellenlänge, bei der die ausgesandte Strahlung eines Schwarzen Strahlers ein Maximum aufweist, bei veränderlicher Temperatur verschiebt. Das WIENsche Verschiebungsgesetz lässt sich durch Differentiation aus der PLANCKschen Gleichung ableiten.

Je geringer die Temperatur des zu messenden Objektes ist, desto weiter verschiebt sich dessen Strahlungsmaximum hin zu größeren Wellenlängen. In der Nähe der Raumtemperatur liegt dieses etwa bei 10 µm.
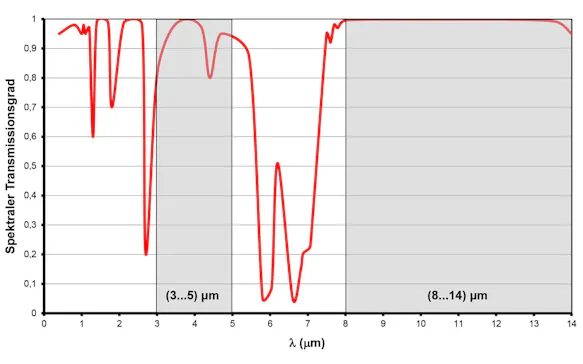
Die Durchlässigkeit (Transmission) der Luft ist sehr stark wellenlängenabhängig. Bereiche mit hoher Dämpfung wechseln sich mit Bereichen hoher Durchlässigkeit (schraffiert), den so genannten "atmosphärischen Fenstern", ab. Während im Bereich (8 ... 14) µm, dem langwelligen atmosphärischen Fenster, die Durchlässigkeit auch über große Entfernungen gleichmäßig hoch ist, treten im Bereich (3 ... 5) µm, dem kurzwelligen atmosphärischen Fenster, bereits bei Messentfernungen von einigen zehn Metern messbare Abschwächungen durch die Atmosphäre auf.
Einflüsse durch das Messobjekt
Der Schwarze Strahler als strahlungsphysikalisches Modell ist für die Betrachtung der grundlegenden Zusammenhänge unerlässlich. Da praktische Messobjekte jedoch mehr oder minder stark von diesem Modell abweichen, ist es ggf. notwendig, diesen Einfluss bei der Messung zu berücksichtigen. Hierfür eignet sich der Parameter des Emissionsgrades, welcher ein Maß für das Vermögen des Körpers ist, Infrarotstrahlung auszusenden. Der Schwarze Strahler besitzt mit dem Wert 1 den größtmöglichen Emissionsgrad, welcher zudem unabhängig von der Wellenlänge ist.
Im Gegensatz dazu kann der Emissionsgrad realer Messobjekte eine mehr oder minder starke Abhängigkeit von der Wellenlänge aufweisen. Zudem ist ein Einfluss folgender Parameter möglich:
Materialzusammensetzung
Oxidschicht auf der Oberfläche
Rautiefe der Oberfläche
Winkel zur Flächennormalen
Temperatur
Polarisationsgrad
Eine Vielzahl nichtmetallischer Stoffe weist – zumindest im langwelligen Spektralbereich - unabhängig von ihrer Oberflächenbeschaffenheit einen hohen und relativ konstanten Emissionsgrad auf. Hierzu gehören die menschliche Haut ebenso wie die meisten mineralischen Bau- und Anstrichstoffe.
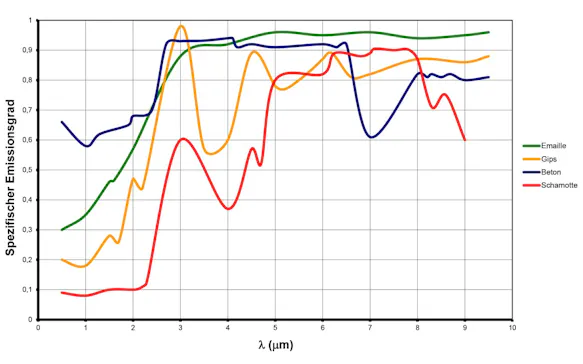
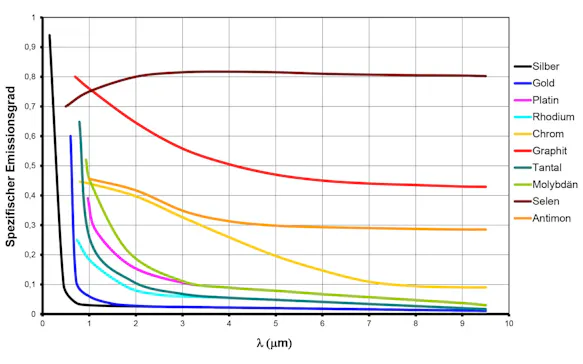
Demgegenüber haben Metalle in der Regel einen niedrigen, stark von der Oberflächenbeschaffenheit abhängigen und zu größeren Wellenlängen hin abfallenden Emissionsgrad.

Möchten Sie mehr erfahren?
Nicht selten sind Aufgabenstellungen mit besonderen Anforderungen verknüpft. Besprechen Sie gemeinsam mit unseren Spezialisten Ihre konkrete Anwendung, erhalten Sie weiterführende technische Informationen oder lernen Sie unsere Zusatzdienstleistungen kennen.
Jetzt anfragen
Literaturverzeichnis
Norbert Schuster, Valentin Kolobrodov
Infrarotthermographie
WILEY-VCH Verlag, Berlin 2000, ISBN 3-527-40130-X
Stahl, K.; Miosga, G.
Infrarottechnik
Hüthig Verlag, Heidelberg 1986
Glückert, Udo
Erfassung und Messung von Wärmestrahlung
Franzis Verlag, München 1992
ISBN 3-7723-6292-3
Wissensspeicher Infrarottechnik
Fachbuchverlag, Leipzig 1990, ISBN 3-343-00498-7
/5/ Walther, L.; Gerber, D.
Infrarotmeßtechnik
Verlag Technik, Berlin 1983
Wolfe, W. L.; Zissis, G. J.
The infrared handbook
Office of Naval Research, Washington 1978
The infrared and electro-optical systems handbook
SPIE Optical Engineering Press, Washington 1993
Lieneweg, F.
Handbuch der technischen Temperaturmessung
Vieweg Verlag, Braunschweig 1976
Touloukian, Y. S.; DeWitt, D. P.
Thermophysical properties of matter
Vol.8: Thermal radiative properties - Metallic elements and alloys
Vol.9: Thermal radiative properties - Nonmetallic solids
IFI / Plenum, New York and Washington 1972
Technische Temperaturmessungen - Strahlungsthermometrie
VDI / VDE-Richtlinie 3511, Fachausschuß 2.6 Technische Temperaturmessung
in VDI / VDE-Handbuch Meßtechnik I, Juni 1993
Gaussorgues, G.
Infrared Thermography (Microwave Technology Series 5)
Chapman & Hall, 1994, London
ISBN 0412479001





